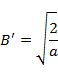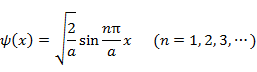2.2 井戸型ポテンシャル内の一次元自由粒子
|
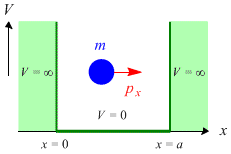
一次元の Schrödinger 方程式 (2.2.1) において,前節の自由粒子では常にポテンシャルエネルギー V を0とおいて計算した。 ここでは,0 < x < a の範囲で V = 0,x ≤ 0,x ≥ a の範囲で V = ∞ となる場合を考える。 |
0 < x < aでは,(2.2.1) は (2.1.4) と同一であり,その一般解は (2.1.8),または (2.2.2) で表される。
|
(2.2.2) |
x ≤ 0,x ≥ a の範囲では ψ = 0 (粒子の存在確率が0)で,かつ,ψ は連続関数でなければならないので,(2.2.2) より
|
(2.2.3) |
さらに,
|
(2.2.4) |
となることから
|
(2.2.5) |
の関係式が得られる。ここで,n = 0 では ψ は常に0となるため無意味であり,n が負の整数の場合も ψ の符号が変わるだけで n が正の場合と同じ状態を表すので考慮しなくてよい。
(2.2.5) を変形するとエネルギーが求められ,
|
となる。(2.2.6) はエネルギー En が0以上の任意の値ではなく離散値をとることを示している。
(2.2.3),(2.2.5) を (2.2.2) に代入すると,
|
(2.2.7) |
となる。規格化条件
|
(2.2.8) |
より B' を求めると
|
(2.2.9) |
である。したがって,波動関数は
|
である。
|
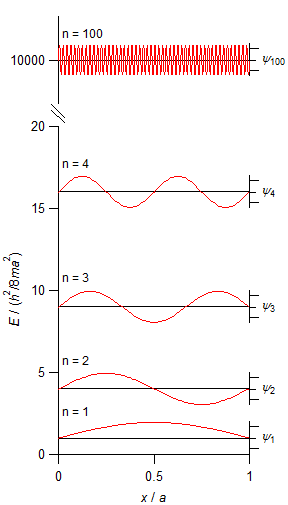
古典的な自由粒子は 0 < x < a の範囲に一様に存在しているが,量子数 n が 1 のときは,x = 0.5a で存在確率が最大になる(|ψ|2 が存在確率を表す)ことに注意する。 n が大きくなると,存在確率は一様になり古典的粒子に近づく。 エネルギーの単位 h2/8ma2 は,a = 1 cm の中にある水素分子を例にとると,m = 2 × 1.661 × 10-27 kg より,1.653 × 10-37 J と計算される。この値は,回転運動のエネルギー単位(3.3 節)と比べて 10-16 も小さいので,事実上エネルギーは連続的な値をとると考えてよい。 |
Revised: 2007-07-02
(2.1.8) から (2.2.2) への変形には Euler(オイラー)の公式
![]()
を利用する。