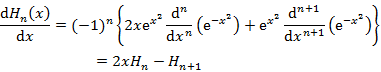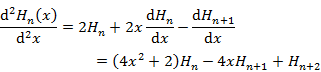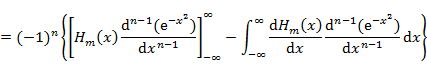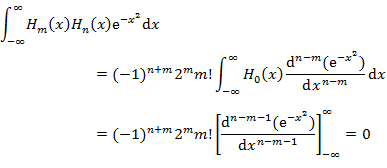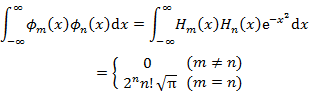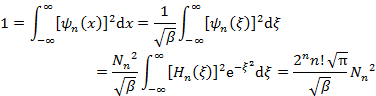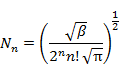4.4.1　Hermite 微分方程式に関する計算

Hermite（エルミート）微分方程式

　微分方程式

の解は

である。(4.4.101) の両辺をさらに (n + 1) 回微分すると，

を得る。ここで，z は

であり，

の形（u(x) は n 次の多項式）をとることがわかる。(4.4.105) を (4.4.103) に代入すると，

を得る。

　(4.4.106) は Hermite 微分方程式として知られ，その解

のうち，c = (-1)ⁿ の特殊解

は n 次の Hermite 多項式とよばれる。

　０次から５次までの Hermite 多項式は以下のようになる。

漸化式の導出

　(4.4.108) の両辺を１階微分，２階微分すると，それぞれ

を得る。(4.4.109)，(4.4.110) を (4.4.106) に代入すると，

となる。(4.4.111) を書き換えて，漸化式

を得る。

直交性の証明

　次に，

が直交系をなすこと，すなわち，

を示す。m < n とし，n について (4.4.108) を (4.4.114) の左辺に代入する。

　(4.4.115) の右辺は次のように書き換えられる。

　(4.4.116) の右辺第１項は，x = ±∞ において であるため 0 である。さらに，(4.4.109) と (4.4.112) から得られる関係式

を (4.4.116) の右辺第２項に代入し，

を得る。(4.4.118) の右辺の積分は，(4.4.115) の積分に含まれる m と n がそれぞれ１減少した形なので，上記の手順を繰り返すと，

となり，直交性が証明される。

　また，m = n の場合は，

である。以上をまとめると，

となる。

調和振動子の波動関数の規格化

　調和振動子の波動関数 ψ は

である（N_n は規格化定数）。規格化条件および (4.4.120) より，

となるので，N_n は，

と求められる。