5.5　動径分布関数

n が 3 までの動径分布関数 R_n,l の具体的な形は以下の通りである。
ここでは，方位量子数 l = 0, 1, 2, ... の順にアルファベット s, p, d, ... で表記している。

n	l	R
1	0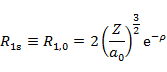
2	0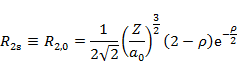
2	1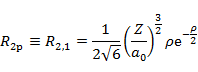
3	0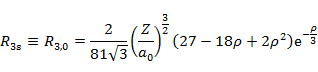
3	1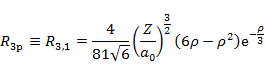
3	2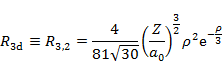

ただし，

水素原子 (Z = 1) の場合の r と R の関係を示したグラフ

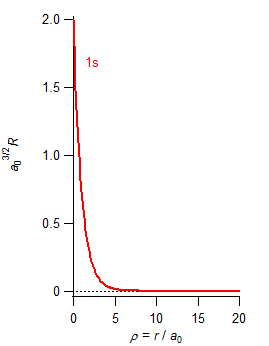	Bohr 半径 　a0 = 5.292 × 10-11 m = 0.5292 Å R = 0 になる点（節点＝node）の数 　n - l - 1 　　　　1s, 2p, 3d → 0 　　　　2s, 3p → 1 　　　　3s → 2

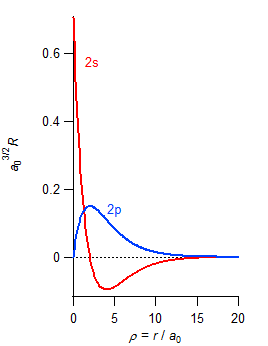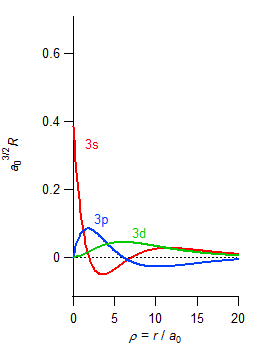　微小空間 dτ に電子を見いだす確率 |ψ|²dτ は，dτ = dxdydz = r² dr sinθ dθ dφ であることから，

となる。いま，核からの距離 r 〜 r + dr の範囲に電子を見いだす確率を P(r)dr とすると，

となる。r と P(r) の関係を図示したのが，次の図である。

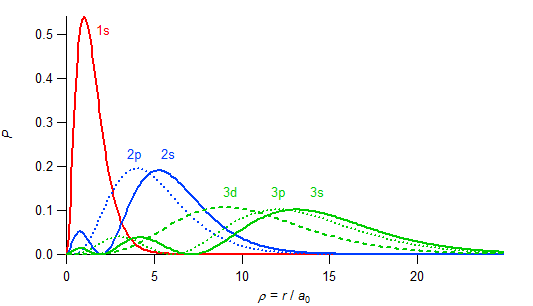
　P(r) は確率分布を表しているので，それぞれの曲線を 0 ≤ r < ∞ の範囲で積分するといずれも1になる。また，主量子数 n が大きくなるにつれて（1 → 2 → 3），核から離れた位置に電子が分布することがわかる。

	P が極大となる r
1s	a0
2s	0.7639a0, 5.236a0
2p	4a0
3s	0.740a0, 4.19a0, 13.07a0
3p	3a0, 12a0
3d	9a0