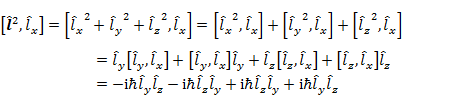1.3　角運動量演算子の交換関係

　ここで，角運動量の成分同士の交換関係を調べておく。一般に，関数 ψ に２つの演算子 と を作用させる場合，作用させる順番を入れ替えても結果が同じになるとは限らない。

　演算子間の交換関係を表すために，(1.3.2) のような交換子を定義する。

　 のとき， と は可換であるという。一般に，古典物理量に対応する演算子 と が可換ならば，同時にこれらの確定値（固有値）をとる状態（固有関数）が存在する。角運動量の x 成分と y 成分の間の交換関係を調べると，

となり，可換ではない。同様に，

である。(1.3.5) 〜 (1.3.7) は，角運動量の x，y，z 成分の中の２成分を同時に決めることはできないことを示している。一方，角運動量の２乗と角運動量の x 成分は，

のように可換であり，y 成分，z 成分に対しても同様である。すなわち，角運動量の２乗と角運動量の x，y，z 成分の中のどれか１つは同時に決定できる。

　いま，z 成分に注目し， と に共通の固有関数を ψ， の固有値を λ， の固有値を μ とすると，

が成り立つ。(1.3.11)，(1.3.12) を満たす ψ，λ，μ をこれから求めていくことにする。