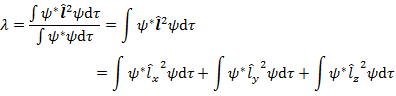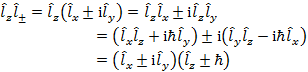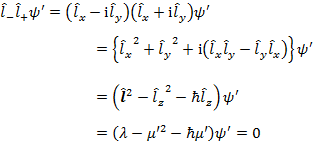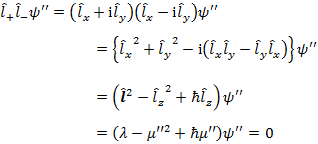1.4　角運動量の z 成分および２乗の固有値

　次の (1.3.11)，(1.3.12) の固有値 λ と μ を求める。

　まず，λ と μ が満たす条件を導く。ψ が (1.4.1) のように規格化されているとすると，(1.3.11) より，λ は (1.4.2) のように表される。

　一般に，古典物理量の演算子 について (1.4.3) の関係が成り立つ（このような演算子をエルミート演算子という）。

　この関係を利用すると，x 成分について

となり，y 成分についても

である。また z 成分については (1.3.12) より，

なので，(1.4.2) より，

の関係が導かれる。

　次に，(1.4.8) で表される演算子（昇降演算子とよぶ）を定義する。

　 の左から を作用させると，

であり，(1.4.9) の両辺を ψ に作用させると，(1.4.10) が導かれる。

　(1.4.10) は が の固有関数で，そのときの固有値が であることを意味している。また，次の (1.4.11) に示されるように， は の固有関数でもあり，固有値は λ である。

　さらに に を作用させた関数も ， の固有関数になる。すなわち，以下のような固有関数と固有値のセットが存在することがわかる。

固有関数	...						...
の固有値	...						...
の固有値	...						...

　(1.4.7) の関係があることから， の固有値 μ には上限と下限が存在する。 の最大固有値を μ'，対応する固有関数を ψ'，また， の最小固有値を μ"，対応する固有関数を ψ" とすると，

である。(1.4.12) の両辺に を，(1.4.13) の両辺に を作用させると，それぞれ

になるため，(1.4.16)，(1.4.17) の関係式が導かれる。

　(1.4.16)，(1.4.17) より，

が得られ， であることから，(1.4.19) に示すように， の最小固有値 μ" は最大固有値 μ' の符号を−にしたものであることがわかる。

　 の固有値は の整数倍だけ変化するので，μ' と μ" の差も の整数倍であり，

結局 (1.4.21) の関係式を得る。

　以上から， の固有値 μ は， の値を取り得ることがわかる。また，(1.4.16)，(1.4.21) より， の固有値 λ は，

となる。従って，(1.3.11)，(1.3.12) は次のように書き換えられる。

　(1.4.23) では l が0以上の整数または半整数となっているが，次に固有関数 ψ を求めていく過程で，0以上の整数のみが許容されることが判明する。