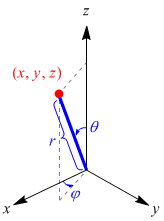
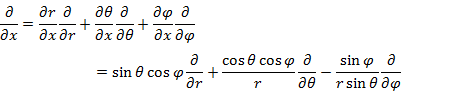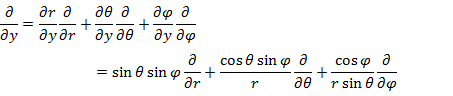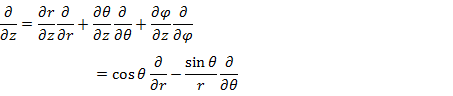1.5　角運動量演算子の極座標表示

　固有関数 ψ を求めるための準備として，座標系を極座標系に変換する。

　微分演算子の変換式

を用いて，直交座標で表された角運動量演算子 (1.2.2)，(1.2.3) を変換すると，次の (1.5.7) 〜 (1.5.10) になる。

　いま求めようとしている と の共通の固有関数 ψ を，長さ r のみに依存する R(r) と角度 θ, φ のみに依存する Y(θ,φ) の積に変数分離する。

　角運動量の２乗に関する式 (1.5.10) と (1.4.23) から，

角運動量の z 成分に関する式 (1.5.9) と (1.4.24) から，

が得られる。なお，(1.5.12) の演算子

を Legendrian（ルジャンドリアン）とよぶことがある。