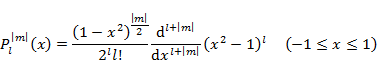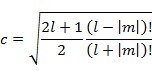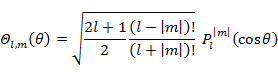1.7 角運動量の z 成分および2乗の固有関数(2)
次に,角運動量の2乗に関する式 (1.5.12) を解く。
|
(1.5.12) |
(1.5.12) の Y を (1.6.1) にしたがって変数分離し整理すると,(1.7.1) のようになる。
|
(1.7.1) |
(1.7.1) の左辺は θ のみ,右辺は φ のみの関数になっているので,両辺は定数でなければならない。実際,右辺は前節で求めた (1.6.11) を代入すると m2 になる。従って,(1.7.1) は,
|
(1.7.2) |
となる。(1.7.2) の解は,l が0以上の整数で l ≧ |m| のときだけ存在し,Legendre(ルジャンドル)の陪多項式 ![]() で表される(解法は省略)。
で表される(解法は省略)。
|
(1.7.3) |
|
(1.7.4) |
(1.7.4) において, c は任意定数である。
(1.6.7) に従って Θ を規格化し c を求めると,
|
(1.7.5) |
となる。
以上をまとめると,
|
となる。ただし,(1.7.8) の R(r) は (1.6.6) の条件を満たす任意の一価連続有限な関数である。
l が2までの具体的な Y は以下の通りである。
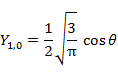 |
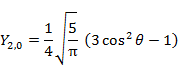 |
|
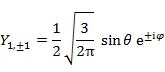 |
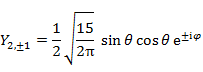 |
|
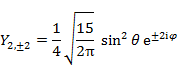 |
Revised: 2007-07-02