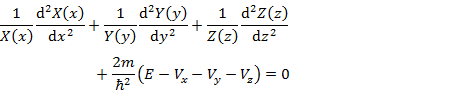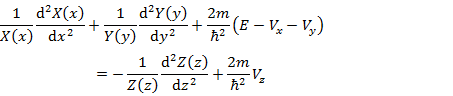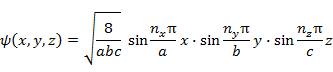2.3 箱の中の三次元自由粒子
|
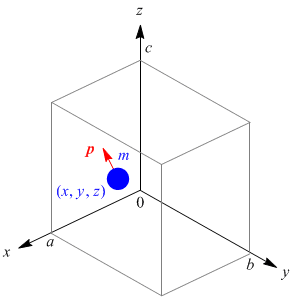
ここでは,前節の一次元の系を三次元に拡張して考える。 箱の中: V = 0 ポテンシャルエネルギー V を x, y, z 成分の和とおく。
Vx = 0 (0 < x < a) |
三次元の Schrödinger 方程式は (2.3.2) である。
|
(2.3.2) |
いま,粒子は自由運動をしているので,x, y, z の各方向の運動は互いに独立している。したがって,波動関数 ψ は x, y, z のそれぞれの一次元関数の積の形における(変数分離)。
|
(2.3.3) |
(2.3.1),(2.3.3) を (2.3.2) に代入すると,(2.3.4) となる。
|
(2.3.4) |
(2.3.4) の z に依存する項のみを移項することが可能であり,(2.3.5) のように変形できる。
|
(2.3.5) |
(2.3.5) の左辺は x と y,右辺は z のみに関係しているので,両辺はある定数に等しい。その定数を k とおくと,z に関する式は (2.3.6) になる。
|
(2.3.6) |
さらに,(2.3.8) にしたがって k を Ez に置き換えて (2.3.6) を変形すると,一次元の式 (2.2.1) と同じ形の (2.3.7) になることがわかる。
|
(2.3.7) | |
ただし, |
|
(2.3.8) |
(2.3.7) を (2.3.5) に代入すると,x と y についても同様の手続きで (2.3.9) のように変数分離できる。
|
|
(2.3.9) |
全エネルギー E が (2.3.10) のように x, y, z 成分の和に表されるとすると,
|
(2.3.10) |
(2.3.9) より,(2.3.7) と同様の x, y についての式 (2.3.11),(2.3.12) を得る。
|
(2.3.11) |
|
(2.3.12) |
(2.3.7),(2.3.11),(2.3.12) の解は (2.2.1) の解 (2.2.10) と同様であり,したがって
|
エネルギーは (2.2.6) より
|
と求められる。
Revised: 2007-07-02