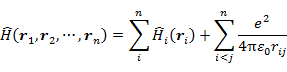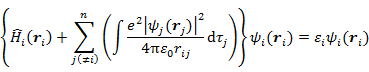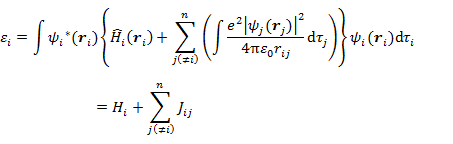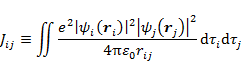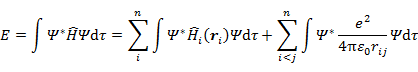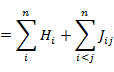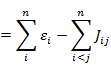7 一般の原子−多電子系
7.1 一般の原子の Hartree 法
n 個の電子をもつ原子の Schrödinger 方程式は,
|
(7.1.1) | |
ただし, |
|
(7.1.2) |
|
(7.1.3) | |
である(ri は核を原点としたときの電子 i の座標)。(7.1.2) の第1項は,(7.1.3) で表される一電子項(電子 i の座標のみに依存)の和,第2項は電子間のクーロン反発を表す二電子項(電子 i と j の座標に依存)の和である。
ここで,ヘリウム原子のところで述べたように,全波動関数を
|
(7.1.4) |
のように個々の電子の座標のみに依存する関数(一電子波動関数)の積の形に近似した場合(一電子近似),最低の全エネルギーを与える一電子波動関数は Hartree 方程式 (7.1.5) を満たす。
|
|
(7.1.5) |
(7.1.5) の{ }内の第2項は電子 i と残りの電子がつくる平均的なクーロン場との相互作用を表している。
Hartree 式 (7.1.5) を解くには,Hamiltonian の中に ψj を含んでいるので ψj があらかじめわかっている必要がある。実際の手順として,はじめに適当な ψj(0) の組を仮定し,それを用いて Hamiltonian を計算した後方程式を解く。得られた新しい解の組 ψj(1) を用いて同じことを繰り返し,ψj(k) が ψj(k-1) と一致したら終了とする(Self-Consistent-Field = SCF 法)。
上述の一電子波動関数 ψi(ri) を「軌道関数(orbital function)」または単に「軌道(orbital)」と呼び,一電子エネルギー εi を「軌道エネルギー(orbital energy)」と呼ぶ。
軌道エネルギー εi は次の式で表される。
|
(7.1.6) |
一電子積分(コア積分)
|
(7.1.7) |
二電子積分(クーロン積分)
|
(7.1.8) |
全電子エネルギー E は次の式で表される。
|
(7.1.9) |
なお,全電子エネルギー E は軌道エネルギー εi の和とはならないことに注意する。(7.1.9) の計算には以下の結果を利用している。
|
(7.1.10) |
|
(7.1.11) |
Revised: 2007-07-27
電子 i と核の距離![]()
電子 i,j 間の距離![]()
原子を扱う場合,ψi(ri) は「原子軌道(atomic orbital = AO)」である。
(7.1.9) の最後の行の変形には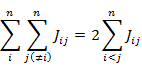
の関係を用いる。