7.2 電子スピン
Hartree 法では，電子は１つずつ軌道関数（一電子波動関数）に割り当てられ（軌道に入り），その軌道関数の積が原子全体の電子状態を表すとしている。しかし実際には，電子状態は軌道の性質（主量子数，方位量子数，磁気量子数の３つの量子数で決まる）のみならず，電子自身がもつ性質（スピン）も考慮してはじめて正しく記述できる。
ここではスピンの概念を天下り的に与えることにする。スピンは下図のように一応「自転」にたとえることができるが，似て非なるものであることに注意する。
|
核の周りを電子がまわる（公転） 電子の自転 |
|
スピン角運動量演算子 
に関しても，角運動量演算子の交換関係（1.3節）が成立するとする。
|
(7.2.1) |
|
(7.2.2) |
|
(7.2.3) |
|
(7.2.4) |
一般の角運動量演算子と同じように，(7.2.1) 〜 (7.2.4) の交換関係から，
と 
に共通の固有関数 ϕ が存在し，(7.2.5)，(7.2.6) が成立することが導かれる（1.3，1.4節参照）。
|
(7.2.5) |
|
(7.2.6) |
ここまでの段階では，スピン量子数 s（軌道角運動量における方位量子数 l に対応）が取りうるのは整数または半整数であるが（式 (1.4.23)），電子スピン角運動量ではこれを 1/2 ただ１つであるとする。したがって，スピン量子数 s とスピン磁気量子数 ms は
|
である。ms が 1/2，-1/2 に対応する固有関数（スピン波動関数）をそれぞれ α，β とすると，
|
(7.2.7) |
|
(7.2.8) |
となる。一般に，α の状態を上向きスピン，β の状態を下向きスピンとよぶ。
|
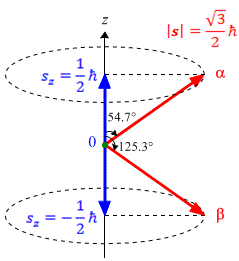
スピン角運動量をベクトルの矢印で図示すると，左のようになる。軌道角運動量のとき（1.8節）と同じように，角運動量の大きさと z 方向の成分は確定するが，x，y 方向の成分は決まらない。 |
|
電子スピンを考慮すると，電子状態を決める量子数は，主量子数 n，方位量子数 l，磁気量子数 m，スピン磁気量子数 ms の４つということになる。 |
Revised: 2007-07-02
核も「自転」していると考えられるので，核スピン角運動量 I が定義できる（磁気モーメントの章を参照）。
電子のスピン量子数 s が 1/2 ということは，スピンに関して取りうる状態の数が 2 ということである（α と β）。このことは Stern と Gerlach により実験的に確かめられており，この実験結果を解釈するためにスピン仮説が導かれた。その後，Dirac によって理論的にも確立された。
スピン量子数 s が半整数の粒子を Fermi 粒子，整数の粒子を Bose 粒子とよぶ。電子，陽子，中性子は Fermi 粒子，光子は Bose 粒子である。