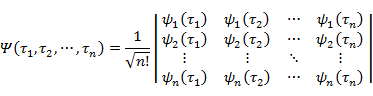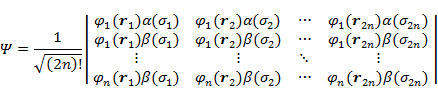7.3　Pauli の原理

　Hartree 法では全波動関数を一電子波動関数の積で近似したが，電子のスピンを考慮すると，それでは不正確であることを以下に述べる。

　多電子系における複数の電子のうち１つを特定して観測することは不可能であり，原理的に電子同士を区別することができない（粒子の同等性）。二電子系（ヘリウム原子）の全波動関数を Ψ とすると，|Ψ|²dτ は dτ に電子１，２を同時に見いだす確率をあらわす。電子１と２の座標をそれぞれ τ₁，τ₂ とすると，２つの電子が区別できないことから，

である。さらに，電子は Fermi 粒子（スピン量子数が半整数）なので，２つの電子を交換したとき全波動関数の符号が変わらなければならないという制約がある。すなわち，

の条件を満たさなければならない。6.2 節，6.3 節で，二電子系（ヘリウム原子）の全波動関数を一電子波動関数の積

とおいて議論したが，(7.3.3) は (7.3.2) の条件を満たしていないことになる。また，6.2 節では２つの一電子波動関数をどちらも同じ水素類似原子の 1s 型軌道としているが，２つの電子が同じ軌道に入れるかどうかは実は自明のことではない（1s 型軌道のエネルギーが一番低いからという理由は考えられるが，ではリチウム原子のような三電子系の３個目の電子もやはり 1s 型軌道に入れるかというと，それは結論から言うとできない）。(7.3.2) の条件を満たすには，全波動関数を

とおけばよい（N は規格化定数）。(7.3.4) で２つの一電子波動関数を同じにすると，

となってしまうので，２つの電子が同じ一電子波動関数で表される状態をとることはない。スピンを考慮した一電子波動関数は，主量子数 n，方位量子数 l，磁気量子数 m，スピン磁気量子数 m_s の４つの量子数で決まる。6.2 節では２つの電子がともに水素類似原子の 1s 型軌道に入るとしていたが，そのときはスピンを考慮していなかった。２つの電子は同じ n = 1，l = 0，m = 0 をもつがスピンが異なる（α と β）とすれば，矛盾はない。

　Ψ の規格化条件より規格化定数を求めると，

となり，二電子系の全波動関数は，

となる（τ₁，τ₂ はスピン座標を含めた座標）

　(7.3.7) を行列式で表現すると，

となる。

　これを n 電子系に拡張すると，全波動関数は

となる（φ_i(r_i) は波動関数の空間座標部分，α(σ_i) と β(σ_i) はスピン波動関数）。(7.3.9) の行列式を Slater（スレーター）行列式 という。

　(7.3.10) を (7.3.9) に代入してスピンをあらわに表現すると，偶数個 2n の電子を含む原子の基底状態に対して次のような式が得られる。

　(7.3.11) の代わりに，簡便のために行列式の対角項だけを記述する場合もある。

　(7.3.9) または (7.3.11) の行列式は，一般的な行列式の性質から，波動関数の満たすべき要請

• 電子の交換（→列の交換）で Ψ の符号が変わる

• ψ_i = ψ_j（→２つの行が一致）は Ψ = 0となるのでありえない

を満たしていることがわかる。２番目の要請を言い換えると，

となる。これを Pauli（パウリ）の排他原理 という。