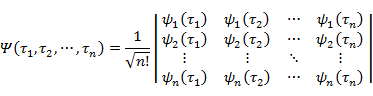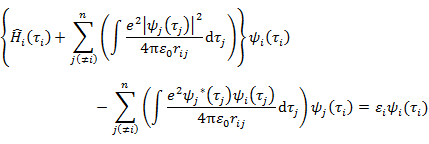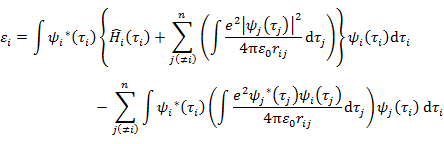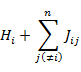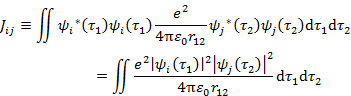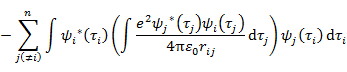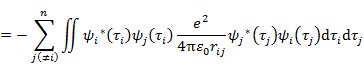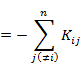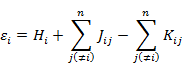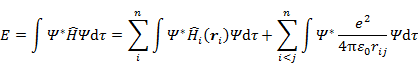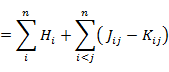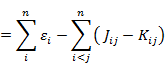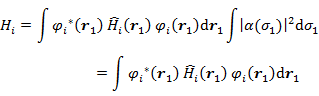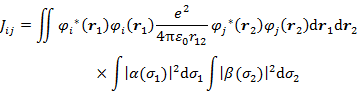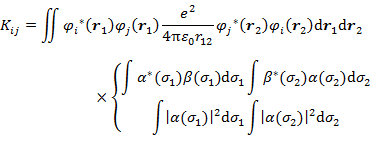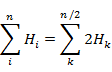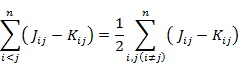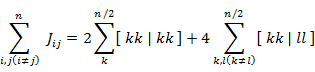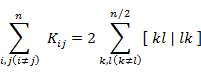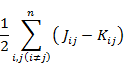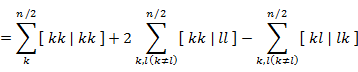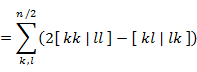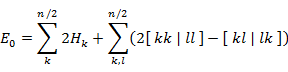7.5　Hartree-Fock 法

　一般の原子の全波動関数を Slater 行列式

で表したとき，最低の全エネルギーを与える一電子波動関数 ψ_i の組は次の Hartree-Fock（ハートリー−フォック）式を満たす。

(7.5.1) は，全波動関数を単純な一電子波動関数の積 (7.1.4) で表したときの Hartree 式 (7.1.5) に対応するものである。(7.5.1) と (7.1.5) の違いは，(7.5.1) の左辺に第２項が加わった点である。

　(7.5.1) の両辺に ψ_i^*(τ_i) を掛けて τ_i について積分すると，一電子エネルギー ε_i は，

となる。(7.5.3) の右辺第１項は，Hartree 法のときの ε_i と同じで，

一電子積分（コア積分）

二電子積分（クーロン積分）

である。(7.5.3) に新たに加わった第２項は，

のように書くことができる。ここで，

は交換積分とよばれる。したがって，ε_i は

である。

　全電子エネルギー E は次の式で表される（解法は煩雑になるので省略）。Hartree 法の全電子エネルギー (7.1.9) と比較すると，交換積分の項が加わっていることがわかる。

　ここで，一電子波動関数 ψ_i(τ_i) を軌道部分 φ_i(r_i) とスピン部分とに分けて上記の各積分を記述してみる。

　コア積分 (7.5.5) に ψ_i(τ_i) = φ_i(r_i)α(σ_i) を代入すると，スピン部分の積分は規格化されているので，

となる。当然，スピンが β の場合でも同様である。

　クーロン積分 (7.5.6) についてもスピン部分の積分は１となる。例えば，α と β の組み合わせでは，

である。これは，α，α または β，β の場合でも同様である。なお，(7.5.12) の最後の行は簡略化した記述である。

　一方，交換積分 (7.5.8) の場合は，スピンの組み合わせによって結果が異なる。いま，α と β（異なるスピンの組み合わせ）とα，α（同じスピンの組み合わせ）のそれぞれについて計算すると，

となる。(7.5.13) ２行目上段は異なるスピン同士の場合で，α と β は直交していることからこの積分は０である。一方，下段の積分は同じ α スピン同士の場合で（β でも同じ），値は１である。したがって，２つの電子のスピンが異なる場合の交換積分は

スピンが同じ場合は，

(7.5.15)

である。

　次に，スピンを考慮して，偶数個の電子をもつ基底状態の原子の全エネルギーを表す式を求める。電子の数が n のとき，被占原子軌道の数は n/2 である。(7.5.10) の２行め第１項（一電子項）を書き直すと，

となる（i は電子の番号，k は原子軌道の番号）。(7.5.10) の２行め第２項（二電子項）

については，２つの電子の軌道とスピンの組み合わせにより以下のように３つのケースが考えられる。

• 電子 i，j は同じ軌道 k に入り，異なるスピン（α，β または β，α）を有する
  　　 　　

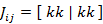
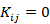
• 電子 i，j は異なる軌道 k，l に入り，異なるスピン（α，β または β，α）を有する
  　　 　　

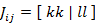
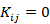
• 電子 i，j は異なる軌道 k，l に入り，同じスピン（α，α または β，β）を有する
  　　 　　

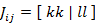
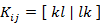
これらを全部足しあわせると，

となるので，全エネルギーの二電子項は，

となる。なお，(7.5.20) の最後の行の変形では k = l のとき次の関係が成り立つことを利用している。

　(7.5.16) と (7.5.20) をまとめると，電子数 n の基底状態にある原子の全エネルギー E₀ は

である（k，l は原子軌道の番号）。