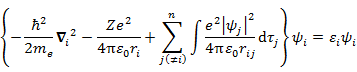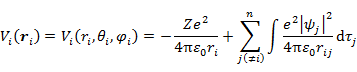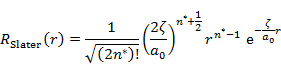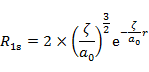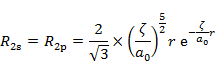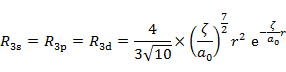7.6　近似原子軌道

　ここでは，原子の一電子波動関数（原子軌道）の近似関数として広く用いられている Slater（スレーター）型原子軌道（Slater-Type Orbital = STO）について述べる。量子化学計算の対象の多くは分子であり，後で述べるように分子の一電子波動関数（分子軌道）は原子軌道の一次結合で近似する。一般に分子の計算では，計算量を少なくするため，原子軌道に含まれる原子ごとのパラメータ（例えばこの節で述べる Slater exponent）を分子を変えるたびに変分法で最適化することはせず，固定値を用いることが多い。

は本来球対称（電子 i の距離 r_i のみに依存）ではないが，問題を簡単にするため球対称とおいてみる。そうすると，(7.6.1) は

となり，水素類似原子の場合と同じように変数分離が可能になる（5.3 節参照）。

　(7.6.4) の中の球面調和関数 Y(θ_i,φ_i) は水素類似原子の場合と同じであるが，動径分布関数 R(r_i) は V_i(r_i) がクーロンポテンシャル型ではないため，正確な解が求められない。

　Slater は R を水素類似原子の場合と類似した関数で近似することを提案した。すなわち，水素類似原子の R は

で表されるが（c は規格化定数），この中の Laguerre の多項式

を r の最高次数（n − l − 1 次）の項のみに置き換えて，改めて規格化を行うようにする。

　さらに，(7.6.5) の中に現れる主量子数 n と核電荷 Z を，それぞれ有効主量子数 n^*，有効核電荷 Z^* に置き換え，Slater exponent を (7.6.7) のように定義する。

　以上の操作を行うと，Slater の R は次の (7.6.8) の形になる（c' は規格化定数）。

(7.6.8) からわかるように，R_Slater は方位量子数 l には依存せず，有効主量子数 n^* のみに依存している。

　Slater は実験値などをもとに，有効主量子数 n^*，有効核電荷 Z^* を次のように定めた（Slater’s rule）。

(1) n^* は次表によって定める。

n	1	2	3	4	5	6
n^*	1	2	3	3.7	4.0	4.2

(2) Z^* = Z − s とし，s（しゃへい定数とよぶ）は次の手順で定める。

まず，電子を次の群に分ける。

1s / 2s, 2p / 3s, 3p / 3d / 4s, 4p / 4d / 4f / 5s, 5p / 5d / 5f / …
ns と np は同じ群，nd，nf は別々の群とする。
同じ群の電子からは１個につき 0.35 の寄与を受ける。ただし，1s の場合のみ 0.30 の寄与とする。
異なる群の電子からの寄与は次のとおりになる。

着目している電子が属する群より外側の群からの寄与はなし。

着目している電子が s, p 群の場合，n が１だけ小さい電子からの寄与は各 0.85，さらに内側の電子からの寄与は各 1.00。

着目している電子が d 群または f 群の場合，内側の電子からの寄与はすべて 1.00。

　1s 軌道（n^* = 1）を例にとると，水素原子では ζ = 1，炭素原子では Z^* = Z − s = 6 − 0.30 = 5.70 なので ζ = 5.70 と計算される（7.7 節末尾の表参照）。

　n^* が 1～3 のとき，R_Slater について規格化を行うと，一般式は

　Slaterの R の形は有効主量子数 n^* のみに依存し，n^* → n，Z^* → Z の置き換えを行うと，(7.6.10) の関数の形は，それぞれ水素類似原子の R_1s，R_2p，R_3d の形に等しいことがわかる（5.5 節参照）。

　球面調和関数 Y は水素類似原子と共通なので，Slater 型波動関数（Slater 型原子軌道 = STO）の外形は水素類似原子の波動関数と同じである（5.7 節参照）。下の表では，r を原子単位（長さの単位を a₀ とする → ζ / a₀ を ζ と置くのに等しい）で表し，主量子数 n，方位量子数 l が共通のグループ内で異なる部分を赤字で示している。

7.6 近似原子軌道 － STO

7.6　近似原子軌道　－　STO