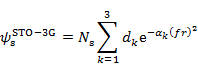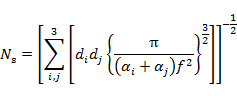7.7　近似原子軌道

7.7　近似原子軌道　－　GTO

　分子の計算に用いる原子軌道関数には，積分計算上の困難さから型関数の代わりに型関数（Gauss 関数）が用いられることが多い。1s の場合，規格化定数も含めると Gauss（ガウス）型原子軌道（Gauss-Type Orbital = GTO）は，

(7.7.1)

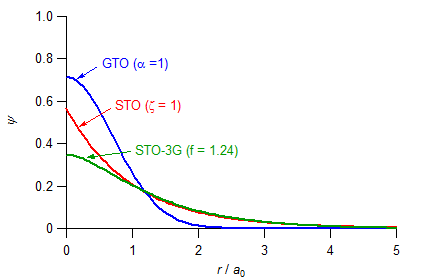
となるが，同じ 1s の Slater 型原子軌道（STO）と比較すると距離 r 依存性が大きく異なる（下図参照）。これを改善するために，(7.7.1) の α が異なる複数の Gauss 関数の線形結合で１つの原子軌道を表現する手法がとられる。この場合の Gauss 関数は計算がしやすいよう，s 型，p 型，d 型の関数として，次の形のものが用いられる（規格化定数は省略）。ここで，α は原子の種類によらない共通の exponent とし，原子による違いは scale factor f で表すことにする。

(7.7.2)

例えば，s 軌道は複数のの線形結合，p_x 軌道は複数のの線形結合で表現する。また，本来 d 軌道は５つであるが，は (7.7.2) に示す６つを使用することが多い。これらの Gauss 関数はもはや１：１で原子軌道と対応していないため，「原子軌道関数」よりむしろ「基底関数」とよぶことが多い。

　STO-3G 基底関数系は３つの Gauss 関数の線形結合で STO を近似した一連の基底関数である。(7.7.3) は STO-3G の s 軌道の一般式，(7.7.4) の N_s は規格化定数である。

	(7.7.3)
	(7.7.4)

水素原子の 1s 軌道

主量子数 n =1, 2 の STO-3G の exponent α_k と係数 d_k

k	n = 1		n = 2
k	α_k	d_k (s)	α_k	d_k (s)	d_k (p)
1	2.2277	0.15433	0.99420	-0.099967	0.15592
2	0.40577	0.53533	0.23103	0.39951	0.60768
3	0.10982	0.44463	0.075139	0.70012	0.39196

STO-3G の標準 scale factor f


Atom	1s	2sp	3sp
H	1.24
He	1.69
Li	2.69	0.80
Be	3.68	1.15
B	4.68	1.50
C	5.67	1.72
N	6.67	1.95
O	7.66	2.25
F	8.65	2.55
Ne	9.64	2.88
Na	10.61	3.48	1.75
Mg	11.59	3.90	1.70
Al	12.56	4.36	1.70
Si	13.53	4.83	1.75
P	14.50	5.31	1.90
S	15.47	5.79	2.05
Cl	16.43	6.26	2.10
Ar	17.40	6.74	2.33

Slater’s rule に基づく Slater exponent ζ


Atom	1s	2sp	3sp
H	1.00
He	1.70
Li	2.70	0.65
Be	3.70	0.975
B	4.70	1.30
C	5.70	1.625
N	6.70	1.95
O	7.70	2.275
F	8.70	2.60
Ne	9.70	2.925
Na	10.70	3.425	0.733
Mg	11.70	3.925	0.95
Al	12.70	4.425	1.167
Si	13.70	4.925	1.383
P	14.70	5.425	1.60
S	15.70	5.925	1.817
Cl	16.70	6.425	2.033
Ar	17.70	6.925	2.25

Revised: 2007-08-05

N_s の値を計算すると，H の 1s 軌道では 0.305115, C の 2s 軌道では 0.275471 となる。

r = 0 において，STO では
dψ/dr ≠ 0 であるが（頂点が尖頭），GTO では dψ/dr = 0 になる（頂点が平ら）。この点は STO-3G でも改善されない。

STO-3G の出典論文

W. J. Hehre, R. F. Stewart, and J. A. Pople, J. Chem. Phys., 51, 2657 (1969).

J. B. Collins, P. v. R. Schleyer, J. S. Binkley, and J. A. Pople, J. Chem. Phys., 64, 5142 (1976).

7.7 近似原子軌道 － GTO

7.7　近似原子軌道　－　GTO