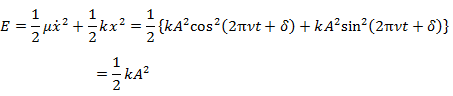4 調和振動子
4.1 調和振動子の古典的エネルギー
|
(x1 > x2) |
二原子分子の振動は調和振動子(いわゆる理想的なバネ)として近似することができる。 全エネルギーは,運動エネルギーとポテンシャルエネルギーの和であるが,調和振動子の場合,古典的エネルギーは以下のようになる。 |
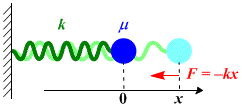
運動エネルギー T
|
(4.1.1) | |
ただし, |
|
(4.1.2) |
第1項=分子の重心の運動エネルギー(並進運動エネルギー)
|
(4.1.3) | |
ただし, |
|
(4.1.4) |
|
(4.1.5) | |
第2項=分子の振動エネルギー
|
(4.1.6) | |
ただし, |
|
(4.1.7) |
|
(4.1.8) | |
平衡核間距離を r0 と置き,それからの変位を ![]() とすると,
とすると,
|
(4.1.9) |
ポテンシャルエネルギー V
|
Hooke の法則より(k は力の定数),
なので,ポテンシャルエネルギーは,
となる。 |
|
x の時間変化は以下のようにして求められる。運動方程式と Hooke の法則より,
|
(4.1.12) |
であるのでこれを解くと,x と t の関係式は (4.1.13) になる(A は振幅)。
|
(4.1.13) | |
ただし, |
|
(4.1.14) |
全エネルギーのうち,並進運動エネルギーを除く内部エネルギー E は
|
(4.1.15) |
となる。内部エネルギーは時間に依存せず,エネルギー保存則が成立していることがわかる。
Revised: 2007-07-02

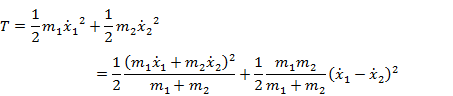
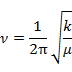 (振動数)
(振動数)