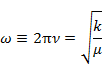4.2　調和振動子の Schrödinger 方程式

　分子内部の振動エネルギーに対応する古典的 Hamiltonian は，(4.1.9) と (4.1.11) の和

で表される（p は運動量）。これを

にしたがって演算子に変換すると

となるので，解くべき Schrödinger 方程式は

である。ここで，k は角振動数 ω と

の関係がある。(4.2.4) の両辺に を掛け，

とおくと，(4.2.4) は

となる。

　まず，x → ±∞，すなわち ξ → ±∞ のときに (4.2.9) を満たす ψ について調べる。この条件では となるので，(4.2.9) は，

と近似できる。ξ → ±∞ で (4.2.10) を満たす ψ は

の形である。このことは，(4.2.11) を (4.2.10) に代入すると，

となることから確認される。ただし，ψ は有限でなくてはならない（|ψ|² は確率をあらわす）ので，(4.2.11) の指数は負のみ有効である。

　以上の考察より，ξ の全領域における ψ の解を次のようにおく。

　(4.2.13) を (4.2.9) に代入すると，u(ξ) についての方程式が得られる。

　(4.2.14) は Hermite（エルミート）微分方程式の形なので，解 u(ξ) は Hermite 多項式として得られる（4.4節）。