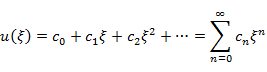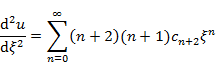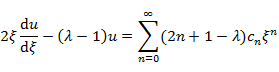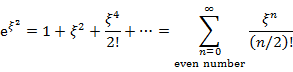4.3　調和振動子のエネルギー

　(4.2.14) の u(ξ) を完全に求める前に，まずエネルギーについて考察する。u(ξ) は多項式として一般に次のように記述できる。

　u(ξ) の１階微分，２階微分を計算し，(4.2.14) の両辺を求めると

となる。左辺と右辺の ξⁿ の係数は常に等しいので，(4.3.2) と (4.3.3) より

の関係式が得られる。

　ここで，u(ξ) が無限級数と仮定すると，(4.3.4) より

となる。一方，

における ξⁿ と ξⁿ+2 の係数の比 cⁿ+2/cⁿ は同様に，

の関係にあるので，ξ → ±∞ のときには u(ξ) は と同様の振る舞いをすることになる。しかし，ξ → ±∞ では は発散してしまうため，

も発散することになり，ψ が有限であることと矛盾が生じる。したがって，(4.3.1) で表される u(ξ) は有限であり，n 次項まで含むとすると，

が成立しなければならない。(4.3.9) より，

の関係が得られ，(4.2.6) と (4.3.10) より，エネルギーの期待値は

と求められる。(4.3.11) はエネルギーが連続値ではなく離散値をとること，および最低エネルギーはゼロではないこと（）を示している。