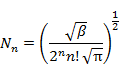4.5　調和振動子の例

調和振動子の波動関数

 (4.4.3)

ただし，

(4.2.8)

(4.4.4)

(4.5.1)

(4.4.6)

調和振動子のエネルギー

 (4.3.11)
n ψ E
0
1
2
3
4
5

水素分子の例

古典論的ポテンシャル

　（単位　V: J，x: m）

H—H の伸縮振動の波数，振動数，角振動数



換算質量

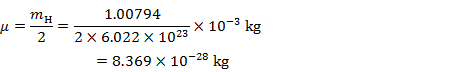
力の定数


　

量子論パラメータ


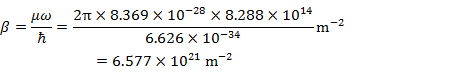
　古典論的ポテンシャル曲線を赤の太線，量子論的エネルギーを赤の細線，波動関数を青の細線で示す。

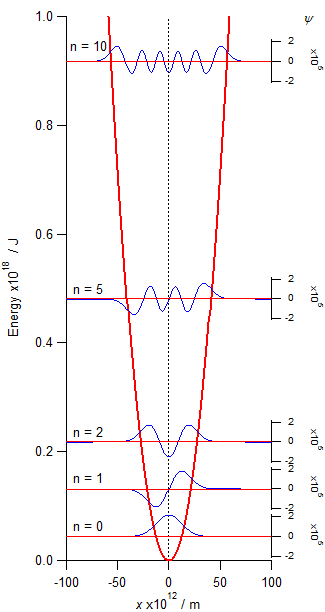ここでわかることは，

  1. 古典的にはエネルギー 0 で振動が止まった状態が存在するが，量子論では最低エネルギー E0 は 0 でなく，この状態は振動を有する（零点振動）。

  2. エネルギー En は離散的で，間隔は一定

  3. 波動関数 ψ の値が 0 になる点（節）は n 個で，エネルギーの増加とともに増加

  4. 平衡構造からの変位 x の平均値は，n が大きくなっても常に 0（平衡構造）

  5. n が大きくなると，波動関数 ψ の絶対値は古典的ポテンシャル曲線上で最大値をとるようになる（平衡構造からの変位の２乗 x2 の平均値は古典的ポテンシャル関数から得られる値と一致）

  6. 波動関数 ψ が古典的ポテンシャル曲線の外側にも値をもつ（トンネル効果）

Revised: 2007-07-04