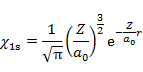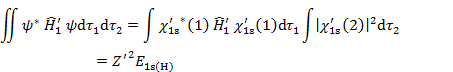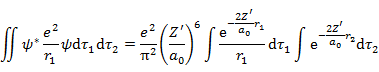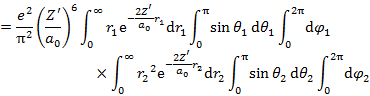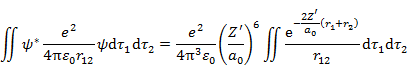6.2 変分法
水素類似原子であるヘリウムイオン(He+)の波動関数(軌道)とエネルギーは正確に求められ,ヘリウムイオンの基底状態(最もエネルギーの低い状態)では,電子は 1s 軌道に入る。
|
(6.2.1) |
(6.2.1) の Z は核電荷であり,ヘリウムイオンでは 2 である。
2電子系であるヘリウム原子の計算では,水素類似原子の波動関数が利用できるように,ヘリウム原子の基底状態の波動関数を各々の電子の 1s 波動関数(一電子波動関数)の積とする。これは,片方の電子の状態は他方の電子の運動に影響されないという近似である(相手電子がどこにあろうと電子状態は変わらないとする)。
|
(6.2.2) |
ただし,電子に作用する核電荷(有効核電荷)はもう1つの電子の存在によって常に2より小さくなると考えられるので,その平均的な核電荷を Z' とおくことにする。Z' を調節可能なパラメータとし,変分法により決定する。一般に,エネルギーが最小となるようにパラメータを決定したときの波動関数はそのパラメータ空間内で最も近似が高いという「変分原理」が成り立つことが知られている。
まず,エネルギー E を Z' の関数として求める。(6.1.2) で表されるヘリウム原子の Hamiltonian H を,(6.1.5) の Z を Z' に置き換えた一電子 Hamiltonian
|
(6.2.3) |
を用いて書き直すと,
|
(6.2.4) |
となるので,エネルギー E は
|
(6.2.5) |
と書ける。(6.2.5) 2行目第1項については,![]() の固有関数が
の固有関数が ![]() ,すなわち
,すなわち
|
(6.2.6) | |
ただし, |
|
(6.2.7) |
が成立し,
|
(6.2.8) |
であるので,
|
(6.2.9) |
である。(6.2.5) 2行目第2項の積分は,
|
(6.2.10) |
|
(6.2.11) |
となる。(6.2.5) 2行目第3項は,
|
(6.2.12) |
となる。なお,ここでは,
|
(6.2.13) |
の式を用いている(解法は省略)。
以上をまとめると,エネルギー E は
|
(6.2.14) |
となる。
E が最小となるための条件
|
(6.2.15) |
より,Z' についての式
|
(6.2.16) |
が得られる。以上の結果は,ヘリウム原子の基底状態の波動関数を (6.2.2) のように水素類似原子(ヘリウムイオン)の 1s 型関数の積で近似する場合,真の核電荷 Z = 2 の代わりに有効核電荷 Z' = 2 - 5/16 = 1.6875 を用いると最良の結果が得られることを示している。
(6.2.16) を (6.2.14) に代入して
|
(6.2.17) |
を得る。この計算値は -77.51 eVで,測定値 -79.006 eV に近い。
Revised: 2007-07-23
ここでは,一電子波動関数(軌道)を表す文字として χ(カイ)を使用する。
一般に N 粒子系で,演算子 ![]() が
が
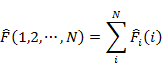
のように各粒子のみに作用する演算子 ![]() の和に分離され,それぞれの
の和に分離され,それぞれの ![]() について
について
![]()
が成立しているとき,
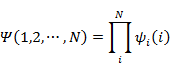
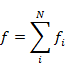
は ![]() の固有関数とそれに対応する固有値である。
の固有関数とそれに対応する固有値である。
極座標系への変換
![]()
積分の計算には次の公式を用いる。
![]()
水素原子の 1s エネルギー
![]()
は,-13.61 eV(5.4 節参照)。