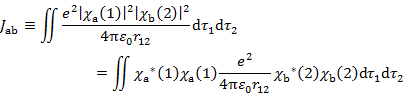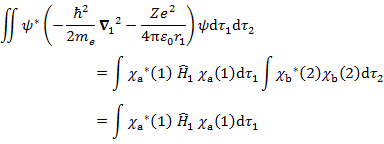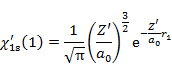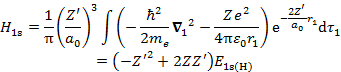6.3　Hartree 法

　前節の変分法の取り扱いでは一電子波動関数に水素類似原子の 1s 型波動関数を用いたが，このことに必然性があるわけではないので，より妥当な任意の形の一電子波動関数を選び，変分法で最小のエネルギーを求めることが可能である。

　ヘリウム原子の全波動関数 ψ を一電子波動関数の積

(6.3.1)

で表現（一電子近似）した場合，全エネルギーを最小にする一電子波動関数は次の Hartree（ハートリー）方程式を満たすことが知られている（導出方法は省略）。

　(6.3.2) の式はそれぞれ電子１，電子２についての方程式になっており，｛ ｝内の Hamiltonian に第２項が新たに加わっている点を除けば，一電子系の水素類似原子の Schrödinger 方程式の形に似ている。

　新たに加わった第２項の積分は電子間反発項であり，着目している電子が他の電子から受ける静電ポテンシャルの平均値を表している（位置の関数ではないことに注意）。しかし，実際は各瞬間で電子同士は互いに避けあってクーロンエネルギーを下げながら「運動」していると考えられるので，Hartree 法で求められるエネルギーは真のエネルギーよりも必ず大きくなる。これが Hartree 法，すなわち一電子近似の限界である。エネルギーが最小となる真の状態と一電子近似の状態の差に基づく効果を電子相関といい，これを考慮した扱いは後述する。

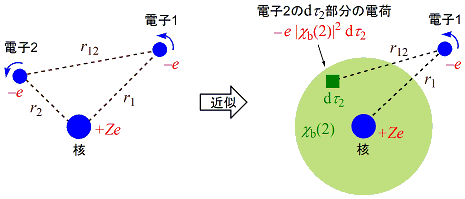
　前節で求めた一電子波動関数も (6.3.2) を満たすが，一般には，(6.3.2) を用いて一電子波動関数を求めることができる。この場合，Hamiltonian の第２項にいま解こうとしている一電子波動関数が含まれているので，最初に適当な可変パラメータを含む χ_a, χ_b の組を仮定して第２項のポテンシャルを計算し連立方程式を解く。更新されたパラメータを含む解の組 χ_a, χ_b を用いて再びポテンシャルを計算し，というように繰り返し計算を行い，計算前後でパラメータに変化がなくなった時点で終了とする。このような繰り返し計算による方法を「つじつまの合う場（Self-Consistent Field = SCF）の方法」と呼ぶ。

　(6.3.2) 右辺の ε_a，ε_b はそれぞれ一電子波動関数 χ_a, χ_b が表す状態のエネルギー（一電子エネルギー）である。ε_a を計算すると，

となる。(6.3.3) ２行目第１項は一電子のみの項で「コア積分」とよばれる。

(6.3.3) ２行目第２項は，微小体積空間での電子１と電子２のクーロン反発に相当しているので，「クーロン積分」とよばれる。

　(6.3.4)，(6.3.5) の記号を用いると，一電子エネルギーは，

となる。全エネルギー E については，全 Schrödinger 方程式

より得られるが，次の積分

を考慮すると，

となる。全エネルギー E は一電子エネルギー ε_a と ε_b の和ではないことに注意する。

　前節の一電子波動関数

についてコア積分とクーロン積分を求めてみると，

となり，一電子エネルギーと全エネルギーは

となる。