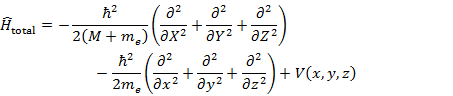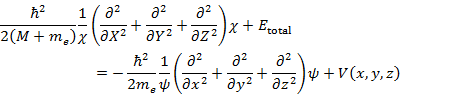5.2　水素類似原子の Schrödinger 方程式

　次に量子化学的な取り扱いをおこなうために，全エネルギー H = T + V を演算子 Hamiltonian に置き換える。

　運動エネルギー T については剛体回転子の場合と同様の変換を行い，ポテンシャルエネルギー V についてはそのまま用いる。一般に，V は核電子間距離 r の関数であり， なので x, y, z の関数とおける。

　原子の並進運動と原子内部の電子の運動は互いに独立していると近似できるので（Born-Oppenheimer 近似），全波動関数 Ψ は (5.2.2) のように X, Y, Z のみの関数 χ と x, y, z のみの関数 ψ の積の形に書ける（変数分離）。

　(5.2.1)，(5.2.2) を Schrödinger 方程式 (5.2.3) に代入し整理すると，(5.2.4) のように書ける。

　(5.2.4) では左辺が X, Y, Z のみの関数，右辺が x, y, z のみの関数になっているので，(5.2.4) が常に成立するためには両辺が定数でなければならない。この定数を E とおくと，(5.2.4) は次の (5.2.5)，(5.2.6) の２つの式に分けて書くことができる。

　(5.2.5) は原子の重心の並進運動についての Schrödinger 方程式で，ポテンシャルエネルギーが０，すなわち自由粒子についての式と同じである。

　(5.2.6) は原子内部の電子についての Schrödinger 方程式で，この式から電子状態を表す波動関数 ψ とエネルギー（電子エネルギー） E が求められる。