5.3 水素類似原子の波動関数とエネルギー(1)
電子についての Schrödinger 方程式
|
(5.2.6) |
または,演算子(ラプラシアン)の記号を使って |
|
|
(5.3.1) |
を解く際にも,剛体回転子のときと同様に極座標に変換する。
ラプラシアンの極座標表示は
|
|
(5.3.2) |
なので,Schrödinger 方程式は
|
(5.3.3) |
となる。電子波動関数 ψ を,次の (5.3.4) のように,長さ r のみに依存する R(r) (動径分布関数)と角度 θ, φ のみに依存する Y(θ,φ) (球面調和関数,角運動量や剛体回転子の計算で出てきたものと同じ)の積に変数分離すると,(5.3.3) は (5.3.5) のように書ける。
|
(5.3.4) |
|
(5.3.5) |
(5.3.5) の左辺は r のみ(動径部分),右辺は θ,φ のみ(角度部分)の関数なので,両辺に等しい定数が存在する。実際,右辺は,既に求められている角運動量の2乗に関する式
|
(5.3.6) |
を利用すると,l(l + 1) に等しいことがわかる。したがって,(5.3.5) の左辺より,r に関する式は
|
(5.3.7) |
となる。ここで注意すべきことは,電子エネルギー E は r のみに関する (5.3.7) を解くことで得られるということである。(5.3.7) は V(r) が (5.1.6) のようなクーロンポテンシャル,すなわち V(r) = -Ze2/4πε0r の場合のみ解け,解は次のようになることが知られている(解法は省略)。
|
|
(5.3.8) | |
|
(5.3.9) | |
ただし, |
|
(5.3.10) |
|
(5.3.11) | |
ここで,![]() は Laguerre(ラゲール)の陪多項式とよばれるもので,(5.3.12) で表される。(5.3.12) の
は Laguerre(ラゲール)の陪多項式とよばれるもので,(5.3.12) で表される。(5.3.12) の ![]() は (5.3.13) で表される Laguerre の多項式である。
は (5.3.13) で表される Laguerre の多項式である。
|
(5.3.12) |
|
(5.3.13) |
また,電子エネルギーは
|
(5.3.14) |
である。
Revised: 2007-07-02
cgs 単位系では,Bohr 半径は
![]()
である。
cgs 単位系では,電子エネルギーは
![]()
である。
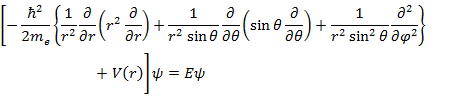
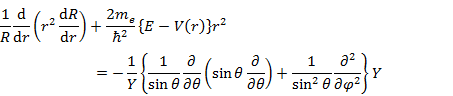
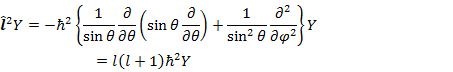
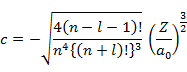 (規格化定数)
(規格化定数)