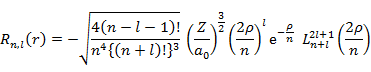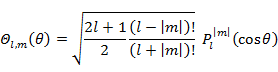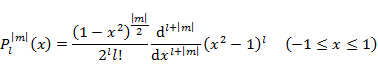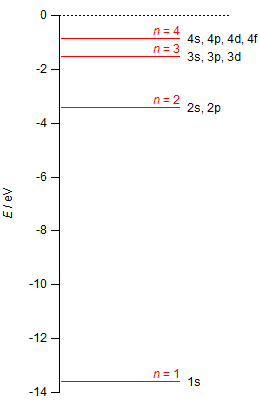5.4　水素類似原子の波動関数とエネルギー（２）

水素類似原子の電子波動関数 ψ

 (5.4.1)

主量子数　
方位量子数　
磁気量子数　

量子数 依存する関数 得られる情報
主量子数 n Rn,l(r) エネルギー，軌道の広がり
方位量子数 l Rn,l(r) と Yl,m(θ,φ) 軌道角運動量の大きさ，軌道の形，
（エネルギー）
磁気量子数 m Yl,m(θ,φ) 軌道角運動量の z 成分

動径分布関数 Rn,l(r)

 (5.4.2)

Laguerre の陪多項式

 (5.4.3)

Laguerre の多項式

 (5.4.4)

(5.3.10)

　　（Bohr 半径）

 (5.3.11)

球面調和関数 Yl,m(θ,φ)

 (5.4.5)

(5.4.6)

Legendre の陪多項式

 (5.4.7)

(5.4.8)

水素類似原子の電子エネルギー E

 (5.3.14)

　電子エネルギー E は主量子数 n の値に応じて離散値を取る。主量子数 n をもつ ψ は n2 個あるので，エネルギーは n2 重に縮重していることになる。

(n,l,m)

n = 1
(1,0,0)

n = 2
(2,0,0)
(2,1,0) (2,1,1) (2,1,-1)

n = 3
(3,0,0)
(3,1,0) (3,1,1) (3,1,-1)
(3,2,0) (3,2,1) (3,2,-1) (3,2,2) (3,2,-2)

　電子エネルギー（Hamiltonian），角運動量の２乗 およびその z 成分 の演算子は互いに可換であることから，電子波動関数 ψn,l,m が示す状態は，電子エネルギー，角運動量の２乗およびその z 成分が同時に確定値 ，， をとる状態である。すなわち，次の (5.4.9) 〜 (5.4.11) は同時に成立する。

 (5.4.9)

(5.4.10)

(5.4.11)

Revised: 2007-07-02

電子波動関数は軌道関数（orbital function）または軌道（orbital）ともよばれる。

方位量子数 l = 0, 1, 2, 3, ... の順にアルファベット s, p, d, f, ... で表記し，s 軌道，p 軌道などとよぶ。

エネルギーは (5.3.7) を解くことで得られるが，水素類似原子以外では，V(r) が単純なクーロンポテンシャルにならないので，一般にエネルギーは方位量子数 l にも依存する。

e = 1.6022 × 10-19 C
a0 = 5.2918 × 10-11 m
ε0 = 8.8542 × 10-12 F m-1
を用いて水素原子の 1s 軌道（Z = 1, n = 1）のエネルギーを計算すると，
E1s = -2.1799 × 10-18 J
である。
また，エネルギーを電子ボルト（eV；電気素量 e を単位とする）で表すと，
E1s = -13.61 eV
である。


(5.3.1) 参照

演算子の可換性については1.3節参照