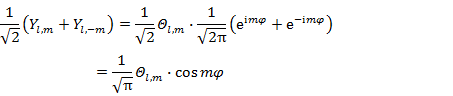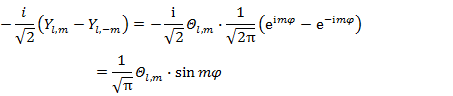5.6　球面調和関数

球面調和関数 Yl,m(θ,φ)

  • 核と電子がなす角度 θ，φ のみに依存する

  • 方位量子数 l と 磁気量子数 m で関数の形が決まる

　球面調和関数 Yl,m(θ,φ) = Θl,m(θ) Φm(φ) の Φm(φ) は m ≠ 0 のとき実関数ではないので，

 (5.6.1)

後の応用のために，Yl,m と Yl,-m の一次結合から２つの互いに直交する実関数 (5.6.2)，(5.6.3) をつくる。

 (5.6.2)

(5.6.3)

　(5.6.2)，(5.6.3) の左辺の係数は規格化定数である。(5.6.2)，(5.6.3) の関数は角運動量の２乗 の固有関数ではあるが，もはや，角運動量の z 成分 の固有関数ではないことに注意する。これらを用いて，l = 2 までの Y を表すと，以下のようになる（元の Yl,m の式は1.7節を参照）。

l |m| Y
0 0
1 0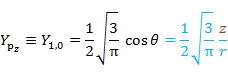
1 1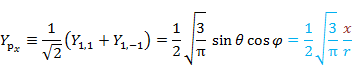
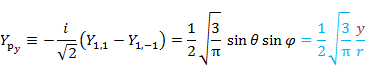2 0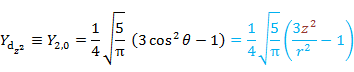
2 1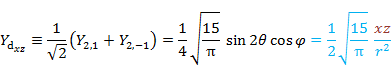
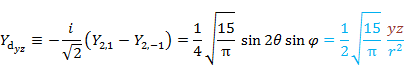2 2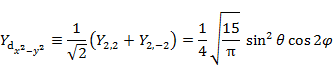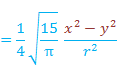

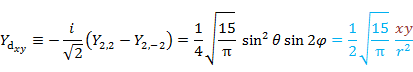Revised: 2007-07-02

球面調和関数 Yl,m(θ,φ) は，角運動量の２乗 と，角運動量の z 成分 の固有関数である（1.7節参照）。

式 (1.5.9)

角運動量の z 成分 の固有関数でないということは，角運動量の（x 成分または y 成分の確定値が得られる代わりに）z 成分の確定値が得られないということ。

式の変形には次の公式を用いる。