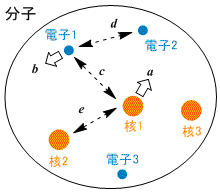
0.1　分子のエネルギーを求めるときの考え方（概要）

分子のエネルギー
＝　核の運動エネルギー（図 a）
　　＋　電子の運動エネルギー（図 b）
　　＋　核−電子の相互作用エネルギー（図 c）
　　＋　電子−電子の相互作用エネルギー（図 d）
　　＋　核−核の相互作用エネルギー（図 e）

核の運動エネルギー　＝　並進運動　＋　回転運動　＋　振動運動

  • 並進運動のモデル　→　自由粒子

  • 回転運動のモデル　→　剛体回転子

  • 振動運動のモデル　→　調和振動子

電子の運動は核の運動に比べて非常に速いので，分子の電子的な性質を考えるときは核が静止していると見なして良い 　＝　Born-Oppenheimer 近似

分子の電子エネルギー　＝　

電子の運動エネルギー Te
＋　核−電子の相互作用エネルギー Vne
＋　電子−電子の相互作用エネルギー Vee
＋　核−核の相互作用エネルギー Vnn

分子の電子エネルギーを求める道筋

  • 水素類似原子（１つの核，１つの電子） Te + Vne

    Schrödinger 方程式が厳密に解け，原子軌道（AO）とエネルギーが求まる

  • 一般の原子（１つの核，２つ以上の電子） Te + Vne + Vee

    一電子近似（Hartree-Fock 近似）の導入
    一電子波動関数（原子軌道，AO）は水素類似原子の AO その他の関数で近似

  • 一般の分子（２つ以上の核，２つ以上の電子） Te + Vne + Vee + Vnn

    一電子近似を適用
    原子の AO に代わるものとして分子軌道（MO）を定義
    MO は構成原子の AO の線形結合で近似（LCAO-MO 近似）

実際の計算法

そのまままともに計算（いわゆる非経験的分子軌道法における Hartree-Fock 法）

近似計算法
（経験的，半経験的分子軌道法）

  • Hückel 法

    π 電子のみを対象
    大胆な近似の導入，定性的

  • PPP 法

    π 電子のみを対象
    色素分子の吸収予測に応用

  • 拡張 Hückel 法

    σ 電子も含めた Hückel 法

  • CNDO 法，INDO 法

    計算対象となる積分をまともに計算せず，原子の物性の実験データをもとにしたパラメータに置換

  • CNDO/S 法，INDO/S (ZINDO) 法

    CNDO 法，INDO 法のパラメータを吸収スペクトルの予測用に最適化

  • MINDO 法

    INDO 法の改良
    分子の実験データからパラメータを最適化

  • MNDO 法，AM1 法，PM3 法

    分子の各種実験データを再現するようにパラメータを最適化

    など

高精度計算法
（Hartree-Fock 近似で考慮されなかった電子相関を考慮）

  • CI (configuration interaction) 法

  • Møller-Plesset の摂動法

    など

Revised: 2008-05-14