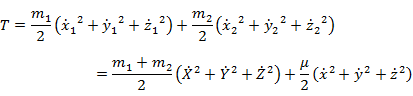3 剛体回転子
3.1 剛体回転子の古典的エネルギー
二原子分子が自由回転するときの波動関数とエネルギーを求める。
剛体回転子(rigid rotator)モデル
自由回転 → ポテンシャルエネルギー V は0
原子1と原子2の結合距離 r は一定
|
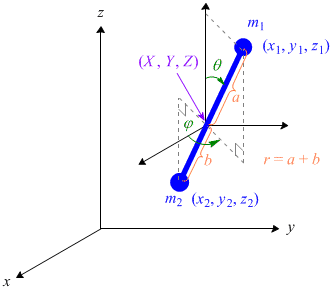
原子1の質量 m1 原子1の座標 (x1, y1, z1) 分子の重心の座標を (X, Y, Z) とし,重心を原点とする局所座標系に極座標 r, θ, φ を用いると,原子1と原子2の座標を6つの独立変数 X, Y, Z, r, θ, φ で表すことができる。
|
原子1
|
(3.1.1) |
|
(3.1.2) |
|
(3.1.3) |
原子2
|
(3.1.4) |
|
(3.1.5) |
|
(3.1.6) |
ここで,
|
(3.1.7) |
|
(3.1.8) |
|
(3.1.9) |
とおいている。
分子の運動エネルギー T
|
(3.1.10) |
ただし, |
|
|
(3.1.11) |
|
(3.1.12) |
(3.1.10) の第1項は分子の(重心の)並進運動のエネルギー,第2項は分子内部の運動エネルギー(ここでは原子間結合距離を一定にしているので回転運動のエネルギーに等しい)である。
第2項は,座標 (x, y, z),質量 μ の粒子の運動エネルギーと等価であることに注意する。
Revised: 2007-07-02