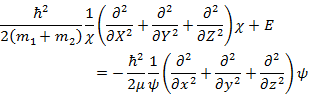3.2　剛体回転子の Schrödinger 方程式

　次に量子化学的な扱いをするために，エネルギーを演算子（Hamiltonian）に置き換える。

　速度と運動量の関係 (3.2.1) を考慮して，古典的運動エネルギーの式 (3.1.10) に対して (3.2.2) のような演算子変換を行うと，Hamiltonian は (3.2.3) となる（自由回転なのでポテンシャルエネルギー V は0である）。

　(3.2.3) の第１項が並進運動，第２項が回転運動に対応しているが，並進運動と回転運動は互いに独立しているので，全波動関数 Ψ は X, Y, Z のみの関数 χ と x, y, z のみの関数 ψ の積とおくことができる（変数分離）。

　(3.2.3) と (3.2.4) を Schödinger 方程式 (3.2.5) に代入して整理すると (3.2.6) となる。

　(3.2.6) の左辺は X, Y, Z のみの式，右辺は x, y, z のみの式になっているので，(3.2.6) が常に成立するためには両辺が定数と等しくなければならない。この定数を E_r とおくと，次の (3.2.7)，(3.2.8) が得られる。

　全エネルギー E を (3.2.9) のようにおけば， (3.2.7) は (3.2.10) となる。

　(3.2.10) は並進運動についての Schödinger 方程式である。この方程式は自由粒子モデルとして解くことができる。

　(3.2.8) が剛体回転子の回転運動についての Schödinger 方程式であり，次の節でこの方程式を解くことにする。