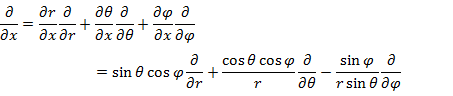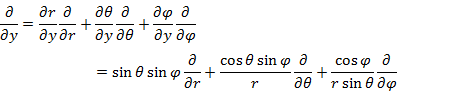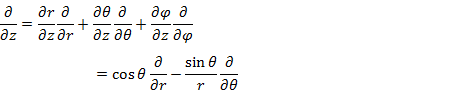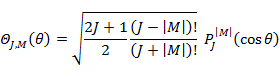3.3 回転運動の波動関数とエネルギー
回転運動の Schödinger 方程式
|
(3.2.8) |
は極座標に変換すると解きやすくなる。まず，(3.1.7) 〜 (3.1.9) より (3.3.1) 〜 (3.3.3) の関係式を得る。
|
(3.3.1) |
|
(3.3.2) |
|
(3.3.3) |
以上の関係式を用いると，(3.2.8) に含まれる演算子（Laplacian）の極座標表示は (3.3.4) になる。
|
|
(3.3.4) |
ここでは，r は一定，すなわち r に対する微分は０となるので，
|
(3.3.5) |
である。(3.3.5) を用いて (3.2.8) を書き換えると (3.3.6) になる（Er の添字は省略）。
|
(3.3.6) |
ここで，I は慣性モーメントである。
|
(3.3.7) |
(3.3.6) の左辺の演算子は (1.5.10) で表される角運動量の２乗の演算子 
である。したがって，波動関数 ψ は，(1.7.9) 〜 (1.7.11) で表される球面調和関数 Y に等しい。
|
||||||||||||||
また，(3.3.6) の固有値 2IE は，
に等しい。したがって，回転のエネルギー E は
|
となる。エネルギー EJ を有する状態は，量子数 M の数，すなわち 2J + 1 だけある。このことを，「2J + 1 重に縮重（または縮退）している」という。
回転エネルギーの単位
|
(3.3.13) |
を回転定数とよぶ。エネルギーは，E0 = 0，E1 = 2B，E2 = 6B，E3 = 12B となる。水素分子（1H–1H）の B の値は，1.218 × 10-21 J，塩化水素分子（1H–35Cl）の B の値は，2.120 × 10-22 J である。
Revised: 2007-07-02
(3.2.8) は並進運動（自由粒子）の方程式 (3.2.10) と同じ形であるが，
が一定であるという条件がついている。
(3.3.1) 〜 (3.3.3) は角運動量の演算子変換（1.5節）で既に出ている。
Laplacian（ラプラシアン）の角度部分（(3.3.5) の｛｝内）は，Legendrian（ルジャンドリアン）とよばれ，Λ2 で表される。
慣性モーメントは回転のしやすさを表す指標である（小さいほど回転しやすい）。一般に，回転中心からの距離の２乗と質量の積を足しあわせた値として定義される。
I = m1a2 + m2b2
重心を回転中心とすれば I は最小となり，(3.3.7) が得られる。
回転運動では，角運動量の量子数の記号 l, m の代わりに，慣習的に記号 J, M を用いる。
一般に，分極している分子は，回転エネルギー準位間（ΔJ = 1）のエネルギー差に等しいエネルギーの電磁波を吸収する。このときの電磁波はマイクロ波領域にあり，塩化水素の場合，E1 – E0 = 2B = 4.240 × 10-22 J に対応する周波数 640 GHz（波数 21.3 cm-1，波長 469 μm）のマイクロ波を吸収する（周波数の値は計算値であり実測値と多少異なる）。
吸収したマイクロ波の周波数から慣性モーメント I が求められるので，分子内の原子間結合距離など分子構造に関するデータを得ることができる。