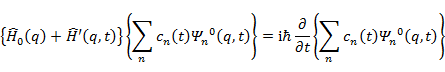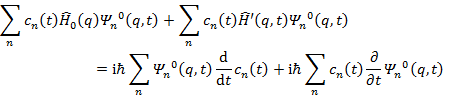10　時間を含む摂動法

10.1　時間を含む摂動法の基礎

　光などの電磁波の放出や吸収を扱う問題では，Hamiltonian や波動関数が時間 t に依存した Schrödinger 方程式を出発点とする（q は電子の座標（スピン座標も含む）を表す）。

　いま，Hamiltonian の時間依存部分を摂動項と考えることにする。

　 の固有関数群を とし，規格直交系を成しているとする。

　時間 t だけ摂動を受けた後の波動関数 を既知である定常状態の波動関数 で展開する。すなわち

とする。時間依存の係数 c_n(t) を求めることが，ここでの命題となる。(10.1.2) と (10.1.5) を (10.1.1) に代入すると，

となり，

となる。(10.1.3) を (10.1.7) に代入して

を得る。(10.1.8) の両辺に左から を掛けて空間座標について積分すると，

となるが， は規格直交系であるため，(10.1.4) にしたがって (10.1.9) の右辺を整理すると，c_m(t) に関する式

を得る。(10.1.10) では右辺にも c_n(t) が含まれているので，このままでは c_m(t) について解くのは困難である。それで，以下に述べるような近似を行う。

　いま，t = 0 のときの状態が n，すなわち，c_n = 1，c_m = 0 (m ≠ n) で

であるとし，時間 t まで摂動 が加わってある状態に変化したとする。十分短い時間内では，やはり c_n ≈ 1，c_m ≈ 0 (m ≠ n) とみなすことができるので，(10.1.10) は次のように書ける。