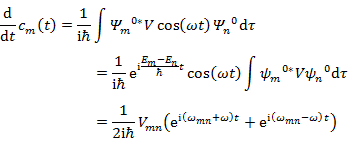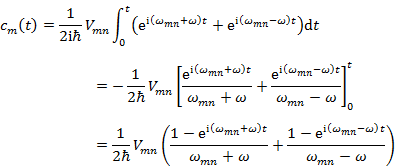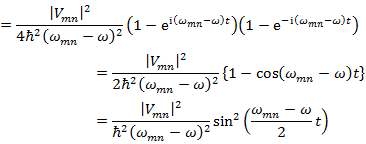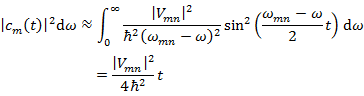10.2　光（電磁波）の吸収と放出（１）

　(10.1.12) の c_m(t) を具体的に求めてみる。

　ここでは，摂動 が時間に対して周期的であるような場合を考える。典型的な例として，原子や分子の光（電磁波）の吸収がある。

　さらに， が，

のように座標のみに依存する と時間のみに依存する に変数分離でき， と に対応する固有値を E_n とする。

　(10.1.3) に (10.2.2)，(10.2.3) を代入すると， 時間依存部分は

となるので， は

となる（定常波の形）。

　さて，(10.2.1) を (10.1.12) に代入し，さらに (10.2.5) を代入すると，

となる。ただし，

である。(10.2.6) の両辺を積分すると，

となるが，摂動が電磁波の吸収の場合，ω は 10⁸ 〜 10¹⁶ s^-1 であるので，(10.2.9) の括弧内の第１項はほぼ 0 である。したがって，(10.2.9) は

と近似できる。なお，ω = ω_mn の場合は，

であるが，(10.2.10) で表される c_m(t) は ω → ω_mn のとき (10.2.11) と同じ値に収束するので，c_m(t) は連続関数である。

　さて，|c_m(t)|² は摂動を時間 t だけ与えたときに状態 m をとる確率を表している。
|c_m(t)|² を計算すると，ω ≠ ω_mn では，

また，ω = ω_mn では，

となる。

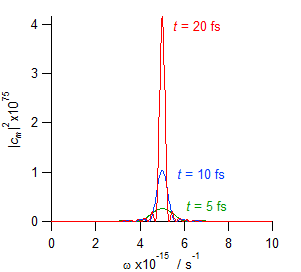|cm|2 と ω の関係 摂動前後のエネルギー差 Em − En が 318 kJ/mol (76 kcal/mol) のとき，ωmn は 5.0 × 1015 s-1 である（式(10.2.8)）。 ω = ωmn 付近で最大値をとり，t が大きくなるほど，シャープになることがわかる。 なお，ω = 5.0 × 1015 s-1 の光は波長 377 nm の紫外線に相当する。また，振動の周期は 1.26 fs (1.26 × 10-15 s) である。

　角振動数が ω 〜 ω + dω の摂動が加わったときに状態 m になる確率は |c_m(t)|²dω で表されるが，上図のように |c_m(t)|² は ω = ω_mn 付近でのみ値をもつ。したがって，状態 m への遷移確率は ω = ω_mn の場合のみ値をもち，その値は角振動数の全領域で積分した値としてよい。

　単位時間あたりの遷移確率は，

となる。