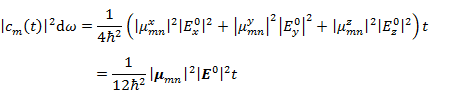10.3 光（電磁波）の吸収と放出（２）
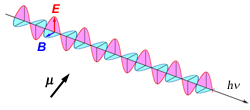
光（電磁波）は，空間の電場 E と磁場 B の変化が波として伝わっていくものなので，(10.3.1) で定義される双極子モーメント μ = (μx,μy,μz) は光により伝えられる電場と相互作用する。
qj は系を構成する j 番目の粒子の電荷，rj は座標である。 |
|
水素原子では，核の座標を原点とすると，双極子モーメントは
|
(10.3.2) |
である。ここで，r = (x,y,z) は電子の位置ベクトルである。
この相互作用を時間によって変化する摂動とみなし，(10.3.3) のようにおくことができる。
|
(10.3.3) |
ここで，
は最大電場を表す。摂動の時間に依存しない部分 V は，
|
(10.3.4) |
で表される。
まず，簡単のため，光の進行方向を z 軸とし，電場ベクトルの方向が x 軸，磁場ベクトルの方向が y 軸である直線偏光を照射した場合を考える。
この場合，E0 の y，z 成分は 0 なので，(10.2.7) の Vmn は，
|
(10.3.5) | |
ただし， |
|
|
である。したがって，
|
(10.3.6) |
となる。一般には，電場は任意の方向を向いているので，
|
(10.3.7) |
であり，また，位相がランダムであるため，|Vmn|2 における交差項は消える。さらに，光は等方性をもっているので，
|
(10.3.8) |
である。したがって，|cm(t)|2 は
|
(10.3.9) |
となる。ここで，
|
(10.3.10) |
で定義される 
を，状態 n から状態 m への遷移モーメントという。
角振動数が ωmn の光のエネルギー密度 ρ(mn) は次式で与えられることが知られている（ε0 は真空中の誘電率）。
|
(10.3.11) |
(10.3.11) を (10.3.9) に代入すると，
|
(10.3.12) |
を得る。さらに，
|
(10.3.13) |
とおくと，単位時間あたりの遷移確率は
|
(10.3.14) |
となる。
ところで，上に記してきた始状態 n と終状態 m を交換しても (10.3.13) と同様の式が得られる。
|
(10.3.15) |
ここで，
|
(10.3.16) |
の関係が成り立つので，
|
(10.3.17) |
である。m ← n の遷移が光の吸収に伴うものとすれば，m → n の遷移は光の放出（発光）に伴うものである。後者は，高いエネルギーをもつ m 状態が ωmn の光の摂動を受けることで同じ ωmn の光を放出してエネルギーの低い n 状態になることを意味し，この過程を誘導放出という。なお，外からの光の摂動を受けることなく光を放出する過程を自然放出という。
Revised: 2007-07-07
m ← n と m → n とで矢印の向きが逆であることに注意。通常，エネルギーの高い状態を左側に書く。