10.4 Einstein の遷移確率
|
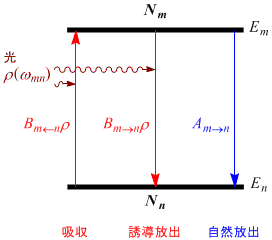
エネルギーが Em の状態と En の状態を有する単一の多数の分子（または原子）が Boltzmann 分布にしたがって分布しているとする。状態 m と n にある個数を，それぞれ Nm，Nn とすると，
(10.4.1) となる。 |
いま，角振動数 ωmn（振動数 νmn）の光を照射したとき，単位時間あたりに n 状態の分子が m 状態に遷移する個数は
|
(10.4.2) |
である。一方，m 状態の分子が n 状態に遷移する個数は，誘導放出と自然放出の両方をあわせて，
|
(10.4.3) |
となる。ここで，自然放出の遷移確率を Am→n とおいた。
定常状態では (10.4.2) と (10.4.3) は等しいので，(10.4.1) を考慮して整理すると，
|
(10.4.4) |
または，
|
(10.4.5) |
となる。(10.3.17) で示したように光吸収と誘導放出の遷移確率は等しいので，
|
(10.3.17) |
(10.4.5) は
|
(10.4.6) |
となる。
一方，絶対温度 T にある黒体から光が放出されるとき，振動数 ν 〜 ν + dν の範囲にある光のエネルギー密度は
|
(10.4.7) |
で表される（Planck の黒体放射の法則）。
を考慮して (10.4.6) と (10.4.7) を比較すると，
|
(10.4.8) |
の関係式を得る。さらに，
|
(10.4.9) |
を (10.4.8) に代入すると，
|
(10.4.10) |
となる。なお，Am→n，Bm→n，Bn→m を Einstein の A 係数，B 係数とよぶ。
(10.4.9)，(10.4.10) から明らかなように，光の吸収・放出に伴って状態 m，n 間の遷移が起こるためには，遷移モーメント μmn が 0 でないことが必要である。
|
μmn ≠ 0 許容遷移（allowed transition） |
Revised: 2007-07-09