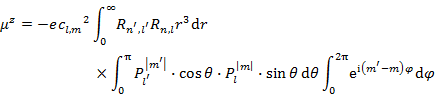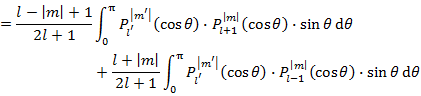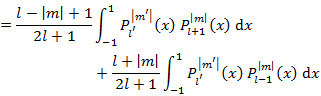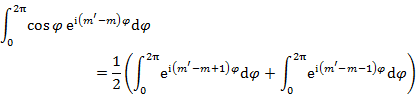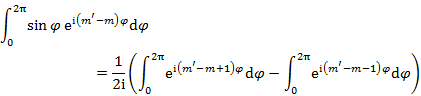10.5 水素原子の電子遷移の選択律
ここでは,水素原子がもつ1個の電子が,光の吸収または放出に伴い軌道間を遷移するときの選択律,すなわち遷移モーメントが 0 にならない条件を導出する。
水素原子の軌道関数は,(10.5.1) に示されるように,動径分布関数 R と球面調和関数 Y の積で表される。
|
(10.5.1) |
|
(10.5.2) |
(10.5.2) の cl,m は規格化定数,P は Legendre 陪多項式である。
いま,量子数 n,l,m の軌道から n',l',m' の軌道へ電子が遷移したとする。このときの遷移モーメント μn',l',m'←n,l,m は
|
(10.5.3) |
である。r =(x,y,z) について
|
(10.5.4) |
|
(10.5.5) |
|
(10.5.6) |
|
(10.5.7) |
の関係式を用いて極座標系に変換する。
まず,z 軸方向の偏光に対する遷移について調べる。遷移モーメントの z 成分は,
|
(10.5.8) |
である。(10.5.8) の右辺の中の r に関する積分が 0 にならないことはすぐわかる。
|
(10.5.9) |
θ に関する積分については,Legendre 陪多項式に関する次の関係式
|
(10.5.10) |
を利用すると,
|
(10.5.11) |
となる(最後に x = cos θ を代入している)。Legendre 陪多項式は直交系を成しているので,積分が 0 にならないためには,l' = l ± 1 かつ |m'| = |m| を満たしていればよい。
φ に関する積分
|
(10.5.12) |
は,m' = m のとき以外は 0 である。以上から,遷移モーメントの z 成分 μz は,l' = l ± 1 かつ m' = m のとき 0 にならないことがわかる。
次に,x 軸,y 軸方向の偏光について調べる。遷移モーメントの x,y 成分の r に関する積分は z 成分の場合と同じである。θ に関する積分
|
(10.5.13) |
は,次の関係式
|
(10.5.14) |
を利用すると,l' = l ± 1 かつ |m'| = |m| + 1 のときに 0 にならないことがわかる。
遷移モーメントの x,y 成分の φ に関する積分はそれぞれ
|
(10.5.15) |
|
(10.5.16) |
であるが,m' = m ± 1 のとき以外は 0 である。
以上をまとめると,
|
水素原子では,方位量子数の変化が Δl = ±1 かつ磁気量子数の変化が Δm = 0 または ±1 を満たす軌道間でのみ光の吸収・放出に伴う電子遷移を起こす。 |
Revised: 2007-07-12